6.11 Carrying Out a Test for the Difference of Two Population Proportions
4 min read•june 18, 2024
Josh Argo
Jed Quiaoit
Josh Argo
Jed Quiaoit
AP Statistics 📊
265 resourcesSee Units
Calculating Values
There are two important values that we need to calculate in order to carry out a test for the difference in two population proportions. We need to calculate a z-score and a p-value. Both need to be included in our response to inference-related FRQs to receive full credit. 💯
Z-Score
The z-score for our test is our critical value. We can calculate it by using the formula for any z-score:
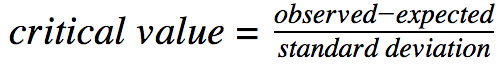
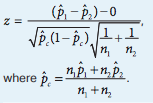
That formula looks pretty icky. 🤢 Luckily if we run our test on a calculator, the z-score is part of our calculator output.
P-Value
As with any p-value, we are using the normal curve and our z-score to calculate the probability of obtaining such a value (or one less than/greater than) that value. Also, using a calculator here is much easier than doing it by hand.
Concluding the Test
Once we have our p-value and z-score, we can then make a judgment to either reject or fail to reject our null hypothesis. ✋
Using P-Value
If you are using a p-value to perform a significance test for the difference in two population proportions, you compare the p-value to the significance level to determine whether to reject the null hypothesis. The significance level is the probability of rejecting the null hypothesis when it is actually true. It is usually set at 0.05, which means that there is a 5% chance of rejecting the null hypothesis when it is actually true.
If the p-value is less than the significance level, it means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. This gives you reason to reject the null hypothesis and conclude that there is a difference between the two population proportions. This means that it was an extremely rare occurrence (WOW value!) and we have reason to believe our null hypothesis (center of our sampling distribution) wasn't accurate.
On the other hand, if the p-value is greater than the significance level, it means that the difference is not statistically significant and may have occurred by chance. In this case, you cannot reject the null hypothesis and must conclude that there is no difference between the two population proportions.
Therefore, if the p is low, reject the H0.
Using Z-Score
If you are using a z-score to perform a significance test for the difference in two population proportions, you can use the empirical rule to determine whether the z-score represents an extremely rare value on the sampling distribution. The empirical rule states that for a normal distribution, approximately 68% of the values fall within one standard deviation of the mean, 95% fall within two standard deviations, and 99.7% fall within three standard deviations. ⭐
So if the z-score is higher than 2 or 3, it is considered an extremely rare value on the sampling distribution, and you can reject the null hypothesis with a high degree of confidence. This means that the difference between the two population proportions is statistically significant and unlikely to have occurred by chance. On the other hand, if the z-score is less than 2 or 3, it is not considered an extremely rare value and you cannot reject the null hypothesis. This means that the difference between the two population proportions is not statistically significant and may have occurred by chance. 🍀
Continued Example
Let's continue our example of MJ vs. Lebron to see if we can verify our conclusion from Unit 6.9. Recall that Michael Jordan made 836/1623 shots and Lebron James made 622/1493 shots. We are seeing if our data gives significant statistical evidence that Michael Jordan is actually better than Lebron. 🏀
Calculations
To avoid the lengthy and cumbersome formulas above, we are going to use a graphing calculator and the appropriate "2 Prop Z Test" to test our hypothesis:
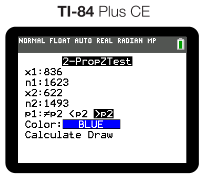
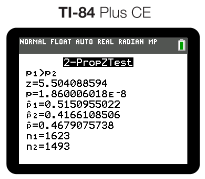
The two big values that we need to write down from our output is our z-score and p-value.
Conclusion
To conclude our test, we can look at how low our p-value is, or how high our z-score is. ➡️
P-Value
Our p-value is the best way to conclude. In this problem, we can see that our p-value is essentially 0. Therefore, we can say:
"Since our p-value is less than 0.05 (~0 < 0.05), we reject our Ho. We have convincing evidence that the true population proportion of shots made by MJ is higher than the true population proportion of shots made by Lebron."
Notice that this supports our conclusion from the confidence interval. ✔️
Z-Score
If not given the data to calculate a p-value or if only given the z-score, we can still make a judgment on the null hypothesis. In the example above, we end up with a z-score of 5.5, which is pretty extreme. Therefore, we can conclude that we can reject our null hypothesis in favor of our alternate hypothesis! ✔️
🎥 Watch: AP Stats - Inference: Hypothesis Tests for Proportions
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

© 2024 Fiveable Inc. All rights reserved.